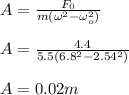Question

A spring with k = 35.5 N/m has a mass of 5.50 kg attached to it. An external force F = (4.40 N)sin[(6.80 s−1)t] drives the spring mass system so that it oscillates without any resistive forces. What is the amplitude of the oscillatory motion of the spring-mass system?

Answer 1

A = 0.02 m

Step-by-step explanation:

The spring constant, k = 35.5 N/m

The attached mass, m = 5.50 kg

The expression for the external force, F = (4.40 N)sin[(6.80 s⁻¹)t].....(1)

The general expression for the external force, F = F₀ sin (wt).............(2)

Comparing equations (1) and (2):

The forced frequency,
`\omega = 6.80 rad/s`

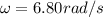
F₀ = 4.40 N

The natural frequency can be calculated using the formula:

`\omega_0 = \sqrt{(k)/(m) } \\\\\omega_0 = \sqrt{(35.5)/(5.5) } \\\\\omega_0 = 2.54 rad/s`

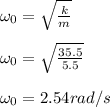
The amplitude of oscillation of a spring-mass system in the steady state:

`A = (F_0)/(m(\omega^2 - \omega_o^2)) \\\\A = (4.4)/(5.5(6.8^2 - 2.54^2)) \\\\A = 0.02 m`