Question

"KATZPSEF1 7.P.053.MI. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Two black holes (the remains of exploded stars), separated by a distance of 10.0 AU (1 AU = 1.50 ✕ 1011 m), attract one another with a gravitational force of 7.70 ✕ 1025 N. The combined mass of the two black holes is 6.00 ✕ 1030 kg. What is the mass of each black hole?"

Answer 1

There are two possible solutions.

M1 = 4.68*10^30kg, M2 = 5.53*10^30kg

M1 = 5.53*10^30kg, M2 = 4.7*10^29kg

Step-by-step explanation:

In order to find the mass of each black hole, you take into account the gravitational force between them and the sum of their masses.

You use the formula for the gravitational force between two masses:

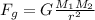`F_g=G(M_1M_2)/(r^2)` (1)

G: Cavendish's constant = 6.674*10^-11 m^3/kg.s^2

M1, M2: mass of each black hole = ?

r: distance between the black holes = 10.0 AU = 10.0(1.50*10^11m) = 1.5*10^12m

Fg: gravitational force between the black holes = 7.70*10^25N

Furthermore, you take into account that the sum of the masses M1 and M2 is:

M1 + M2 = 6.00*10^30 kg (2)

You solve the equation (2) for M2.

`M_2=6.00*10^(30)-M_1`

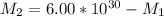
Next, you replace the obtained expression for M2 into the equation (1) and solve for M1, as follow (for simplicity, you do not add the units):

`F_g=G(M_1(6.00*10^(30)-M_1))/(r^2)\\\\(r^2F_g)/(G)=6.00*10^(30)M_1-M_1^2\\\\((1.5*10^(12))^2(7.70*10^(25)))/((6.674*10^(-11))=6.00*10^(30)M_1-M_1^2\\\\2.59*10^(60)=6.00*10^(30)M_1-M_1^2\\\\M_1^2-6.00*10^(30)M_1+2.59*10^(60)=0`

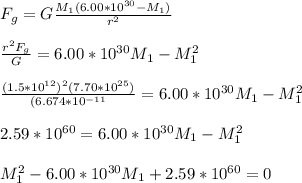
Then, you have obtained a quadratic polynomial. You solve it with the quadratic formula:

`M_1=\frac{-(-6.00*10^(30))\pm \sqrt{(-6.00*10^(30))^2-4(1)(2.59*10^(60)))}}{2(1)}\\\\M_1=(6.00*10^(30)\pm 5.06*10^(30))/(2)\\\\M_1=4.68*10^(29)\\\\M_1=5.53*10^(30)`

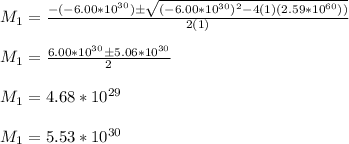
Both results are consistent, then the mass of one black hole can be 4.68*10^30kg and also 5.53*10^30kg.

The other black hole has a mass of:

`M_2=6.00*10^(30)kg-4.68*10^(29)kg=5.53*10^(30)kg\\\\M_2=6.00*10^(30)kg-5.53*10^(30)kg=4.7*10^(29)kg`

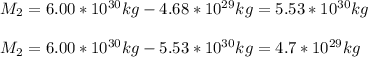
Hence, you have a pair of solutions:

M1 = 4.68*10^30kg, M2 = 5.53*10^30kg

M1 = 5.53*10^30kg, M2 = 4.7*10^29kg