Complete Question:
Given
![\sigma = \left[\begin{array}{ccc}10&12&13\\12&11&15\\13&15&20\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/l6ax98mkhmpwykn0fag368vkq7puxb533i.png) at a point. What is the force per unit area at this point acting normal to the surface with
at a point. What is the force per unit area at this point acting normal to the surface with
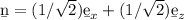 ? Are there any shear stresses acting on this surface?
? Are there any shear stresses acting on this surface?
Answer:
Force per unit area,
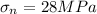
There are shear stresses acting on the surface since
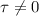
Step-by-step explanation:
![\sigma = \left[\begin{array}{ccc}10&12&13\\12&11&15\\13&15&20\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/l6ax98mkhmpwykn0fag368vkq7puxb533i.png)
equation of the normal,
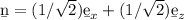
![\b n = \left[\begin{array}{ccc}(1)/(√(2) )\\0\\(1)/(√(2) )\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/79aofozy0kuxdzd6nsbsxzcplu24lvfkgh.png)
Traction vector on n,
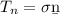
![T_n = \left[\begin{array}{ccc}10&12&13\\12&11&15\\13&15&20\end{array}\right] \left[\begin{array}{ccc}(1)/(√(2) )\\0\\(1)/(√(2) )\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/r46o8ykjsl8pzsag9bndh3uowe8ka3rymi.png)
![T_n = \left[\begin{array}{ccc}(23)/(√(2) )\\0\\(27)/(√(33) )\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/ojrmzdr3l91kmgu96t3gccv5m404n6i384.png)
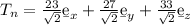
To get the Force per unit area acting normal to the surface, find the dot product of the traction vector and the normal.
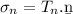
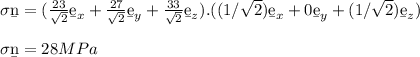
If the shear stress,
 , is calculated and it is not equal to zero, this means there are shear stresses.
, is calculated and it is not equal to zero, this means there are shear stresses.
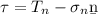
![\tau = [(23)/(√(2) ) \b e_x + (27)/(√(2) ) \b e_y + (33)/(√(2) ) \b e_z] - 28( (1/ √(2) ) \b e_x + (1/ √(2)) \b e_z)\\\\\tau = [(23)/(√(2) ) \b e_x + (27)/(√(2) ) \b e_y + (33)/(√(2) ) \b e_z] - [ (28/ √(2) ) \b e_x + (28/ √(2)) \b e_z]\\\\\tau = (-5)/(√(2) ) \b e_x + (27)/(√(2) ) \b e_y + (5)/(√(2) ) \b e_z](https://img.qammunity.org/2021/formulas/physics/college/v591nb5v2swzfqoerb8kijrixul85fnn1l.png)
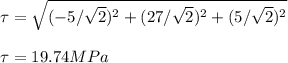
Since
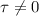 , there are shear stresses acting on the surface.
, there are shear stresses acting on the surface.