Question

In circle o, the length of radius OL is 6 cm and the length

of arc LM is 6.3 cm. The measure of angle MON is 75º.
Rounded to the nearest tenth of a centimeter, what is the
length of arc LMN?
L
0 7.9 cm
6.3 cm
O 10.2 cm
6 cm
M
0 12.6 cm
0 14.2 cm
0 75
N

Answer 1

14.2

Explanation:

Edge

Answer 2

14.2cm

Explanation:

The diagram representing the circle and its attributes has been attached to this response.

As shown in the diagram;

The circle is centered at o,

The length of radius OL = 6cm

The length of the arc LM = 6.3cm

The angle MON = 75°

The angle LOM = θ

Remember that;

The length, L, of an arc is given by;

L = (θ / 360) x (2πr) -------------(i)

Where;

θ is the angle subtended by the arc

r = radius of the circle.

Using the formula in equation (i), let's calculate the angle θ subtended by arc LM as follows;

L = (θ / 360) x (2πr)

Where;

L = length of arc LM = 6.3cm

r = radius of the circle = length of radius OL = 6cm

Substitute these values into the equation to get;

6.3 = (θ / 360) x (2 x π x 6)

6.3 = (θ / 360) x (12 x π)

6.3 = (θ / 30) x (π) [Take π = 22/7]

6.3 = (θ / 30) x (22 / 7)

θ =
`(6.3*30*7)/(22)`

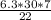
θ = 60.14°

Therefore, the angle subtended by arc LM is 60.14°

Now, from the diagram,

The angle subtended by arc LMN is;

θ + 75° = 60.14° + 75° = 135.14°

Let's now calculate the length of arc LMN using the same equation (i)

L = (θ / 360) x (2πr)

Where;

L = length of arc LMN

θ = angle subtended by LMN = 135.14°

r = radius of the circle = length of radius OL = 6cm

Substitute these values into the equation;

L = (135.14° / 360°) x (2 x π x 6) [Take π = 22/7]

L = 14.15cm

Therefore, the length of arc LMN is 14.2cm to the nearest tenth.