Answer:
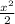 square units [one-half x squared square units]
square units [one-half x squared square units]
Explanation:
As shown in the diagram attached to this response,
Since a square has all sides equal, let the sides of the square be each of a units.
The area, A, of the square = a x a = a²
i.e
A = a² --------------(i)
Now,
The diagonal is x units such that applying Pythagoras rule gives;
x² = a² + a²
x² = 2a²
a² =
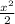 ----------------(ii)
----------------(ii)
Substitute the value of a² in equation (ii) into equation (i) to get;
A =
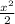
Therefore, the area of the square is
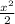 square units
square units