Question

90% of flights depart on time. 80% of flights arrive on time. 75% of flights depart on time and arrive on time. Are the events, departing on time and arriving on time, independent?

Answer 1

Complete Question

90% of flights depart on time. 80% of flights arrive on time. 75% of flights depart on time and arrive on time.

• You are meeting a flight that departed on time. What is the probability that it will arrive on time?

• You have met a flight, and it arrived on time. What is the probability that it departed on time?

• Are the events, departing on time and arriving on time, independent?

Answer:

1st Question

`P(X_1) = 0.833`

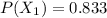
2nd Question

`P(X_2) = 0.938`

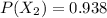
3rd Question

The probabilities are not independent

Explanation:

From the question we are told that

The probability of flight that depart on time is P(DT) = 0.9

The probability of flights that arrive on time is
`P(AT) = 0.8`

The probability of flight that depart on time and arrive on time is
`P(DT\ |\ AT) = 0.75`

In the first question the flight is departed on time so the probability that it will arrive on time is

`P(X_1) = (P(DT\ | \ AT))/(DT)`

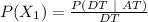
substituting values

`P(X_1) = (0.75)/(0.9)`

`P(X_1) = 0.833`

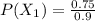
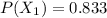
In the second question the flight arrived on time, so the probability that it departed on time is mathematically evaluated as follows

`P(X_2) = (P(DT\ | \ AT))/(AT)`

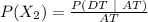
substituting values

`P(X_2) = (0.75)/(0.8)`

`P(X_2) = 0.938`

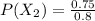
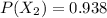
Looking at the given and calculated values we see that the probability of depart on time and arrive is not equal to the probability of depart on time,

i.e 0.75 = 0.8

the probability of depart on time and arrive, and the probability of depart on time are not independent