Answer:
The probability that there are 2 or more fraudulent online retail orders in the sample is 0.483.
Explanation:
We can model this with a binomial random variable, with sample size n=20 and probability of success p=0.08.
The probability of k online retail orders that turn out to be fraudulent in the sample is:
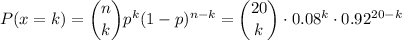
We have to calculate the probability that 2 or more online retail orders that turn out to be fraudulent. This can be calculated as:
![P(x\geq2)=1-[P(x=0)+P(x=1)]\\\\\\P(x=0)=\dbinom{20}{0}\cdot0.08^(0)\cdot0.92^(20)=1\cdot1\cdot0.189=0.189\\\\\\P(x=1)=\dbinom{20}{1}\cdot0.08^(1)\cdot0.92^(19)=20\cdot0.08\cdot0.205=0.328\\\\\\\\P(x\geq2)=1-[0.189+0.328]\\\\P(x\geq2)=1-0.517=0.483](https://img.qammunity.org/2021/formulas/mathematics/college/wj2gh9o1himw6ov54vmv4494o293kqn14o.png)
The probability that there are 2 or more fraudulent online retail orders in the sample is 0.483.