Question

A wave is described by the equation y(x, t) = 35 sin (2 π x - 3 t +1.5), where all numerical values and variables have the appropriate units to produce displacement in cm, speed in cm/s, and time in seconds. What is the speed of the wave?

Answer 1

v = 0.477m/s

Step-by-step explanation:

You have the following wave function:

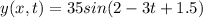`y(x,t)=35sin(2\pix-3t+1.5)` (1)

where y is the vertical displacement of the wave for the position x.

The general form of a wave function can be written as follow:

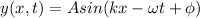`y(x,t)=Asin(kx-\omega t+\phi)` (2)

by comparing the equation (2) and (1) you have:

A: amplitude of the wave = 35

k: wave number = 2π

w: angular frequency of the wave = 3

φ: phase of the wave = 1.5

The speed of the wave is given by the following formula:

`v=(\omega)/(k)`

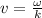
you replace the values of the parameters in the previous formula:

`v=(3)/(2\pi)=0.477(m)/(s)`

The speed of the wave is 0.477m/s