Answer:
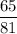 or 80.25%
or 80.25%
Explanation:
Number of blue Marbles = 4
Number of Red Marbles = 5
Total Number of marbles =4+5=9
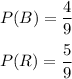
In the experiment, two marbles are chosen one after the other with replacement.
The possible outcomes are: BB, BR, RB and RR
The probability of getting at least 1 red
=P(BR or RB or RR)
=P(BR)+P(RB)+P(RR)
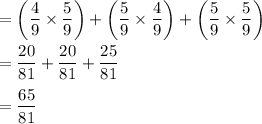
Expressed as a percentage, we have:
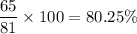
The probability of getting at least 1 red is 80.25%.