Answer:
See Explanation Below
Explanation:
Given
Total Sweets = 10
Red = 4
Green = 2
Yellow = 3
Purple = 1
Required
a & b
The question is not properly presented; however the solution is as follows;
A.
Let P(Yellow) represent the probability of selecting a yellow sweet and n(Yellow) represent the number of Yellow sweets;
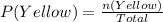
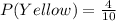
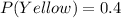
So, whichever letter that shows
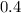 or
or
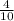 is the probability of choosing a yellow sweet
is the probability of choosing a yellow sweet
B.
Let P(Orange) represent the probability of selecting an orange sweet and n(Orange) represent the number of orange sweets;
Since, there's no orange sweet in the bag;
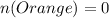
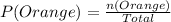
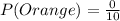
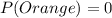
In probability; opposite probabilities add up to 1;
Let P(Not\ Orange) represent the probability of choosing a sweet that is not orange
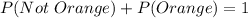
Substitute
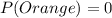


So, whichever letter that shows 0 is the probability of choosing a sweet that is not orange