Answer:
No. At a significance level of 0.1, there is not enough evidence to support the claim that the bags are underfilled (population mean significantly less than 418 g.)
Explanation:
This is a hypothesis test for the population mean.
The claim is that the bags are underfilled (population mean significantly less than 418 g.)
Then, the null and alternative hypothesis are:
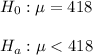
The significance level is 0.1.
The sample has a size n=9.
The sample mean is M=413.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=20.
The estimated standard error of the mean is computed using the formula:
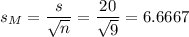
Then, we can calculate the t-statistic as:
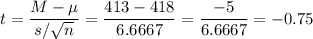
The degrees of freedom for this sample size are:
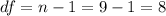
This test is a left-tailed test, with 8 degrees of freedom and t=-0.75, so the P-value for this test is calculated as (using a t-table):
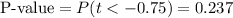
As the P-value (0.237) is bigger than the significance level (0.1), the effect is not significant.
The null hypothesis failed to be rejected.
At a significance level of 0.1, there is not enough evidence to support the claim that the bags are underfilled (population mean significantly less than 418 g.)