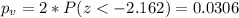Question

A publisher reports that 31% of their readers own a particular make of car. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 100 found that 21% of the readers owned a particular make of car. Determine the P-value of the test statistic. Round your answer to four decimal places.

Answer 1

`z=\frac{0.21 -0.31}{\sqrt{(0.31(1-0.31))/(100)}}=-2.162`

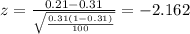
Since is a bilateral test the p value would be:

`p_v =2*P(z<-2.162)=0.0306`

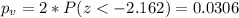
Explanation:

Information given

n=100 represent the random sample taken

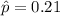`\hat p=0.21` estimated proportion of the readers owned a particular make of car

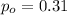`p_o=0.31` is the value that we want to test

z would represent the statistic

`p_v` represent the p value

Hypothesis to test

We need to conduct a hypothesis in order to test if the true proportion is 0.31 or no.:

Null hypothesis:
`p=0.31`

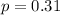
Alternative hypothesis:
`p \\eq 0.31`

The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

And replacing we got:

`z=\frac{0.21 -0.31}{\sqrt{(0.31(1-0.31))/(100)}}=-2.162`

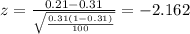
Since is a bilateral test the p value would be:

`p_v =2*P(z<-2.162)=0.0306`