Question

The high temperatures (in degrees Fahrenheit) of a random sample of 6 small towns are: 99 97.5 97.9 99.4 97 97.7 Assume high temperatures are normally distributed. Based on this data, find the 95% confidence interval of the mean high temperature of towns. Enter your answer as an open-interval (i.e., parentheses) accurate to two decimal places (because the sample data are reported accurate to one decimal place).

Answer 1

What are the option for the question

Answer 2

The 95% confidence interval for the mean high temperature of towns is approximately (97.66, 99.50)

How to calculate confidence interval

To find the 95% confidence interval of the mean high temperature of towns based on the given data, use the formula below

`CI = \bar{x} \± (t * (s/\sqrt n))`

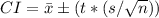
Where:

CI represents the confidence interval

`\bar{x}` is the sample mean

t is the critical value from the t-distribution for the desired confidence level and degrees of freedom

s is the sample standard deviation

n is the sample size

Given data:

Sample size (n) = 6

Sample mean (
`\bar{x}`) = (99 + 97.5 + 97.9 + 99.4 + 97 + 97.7) / 6 ≈ 98.58 (rounded to two decimal places)

To calculate the sample standard deviation (s),

compute the differences between each temperature value and the sample mean,

square those differences,

sum them up,

divide by (n-1), and

take the square root:

`s= \sqrt((99-98.58)^2 + (97.5-98.58)^2 + (97.9-98.58)^2 + (99.4-98.58)^2 + (97-98.58)^2 + (97.7-98.58)^2)/(6-1)]`

s ≈ 0.877

Next, determine the critical value (t) for a 95% confidence level with 5 degrees of freedom (n-1).

Using a t-table, t ≈ 2.571

Now plug in the values into the confidence interval formula:

CI = 98.58 ± (2.571 * (0.877/√6))

CI ≈ 98.58 ± (2.571 * 0.358)

CI ≈ 98.58 ± 0.921

Therefore, the 95% confidence interval for the mean high temperature of towns is approximately (97.66, 99.50) (rounded to two decimal places).