Question

Large samples of women and men are​ obtained, and the hemoglobin level is measured in each subject. Here is the​ 95% confidence interval for the difference between the two population​ means, where the measures from women correspond to population 1 and the measures from men correspond to population​ 2: negative 1.76 g divided by dL less than mu 1 minus mu 2 less than minus 1.62 g divided by dL. Complete parts​ (a) through​ (c) below.

a. What does the confidence interval suggest about equality of the mean hemoglobin level in women and the mean hemoglobin level in​ men? Because the confidence interval does not include includes nothing​, it appears that there is is not a significant difference between the mean level of hemoglobin in women and the mean level of hemoglobin in men. ​(Type an integer or a decimal. Do not​ round.)
b. Write a brief statement that interprets that confidence interval.
A. There is​ 95% confidence that the interval from minus 1.76 g divided by dL to minus 1.62 g divided by dL actually contains the value of the difference between the two population means left parenthesis mu 1 minus mu 2 right parenthesis .
B. There is​ 95% confidence that the difference between the two population means left parenthesis mu 1 minus mu 2 right parenthesis is either minus 1.76 g divided by dL or minus 1.62 g divided by dL .
C. There is​ 95% confidence that the difference between the two population means is not 0.
D. There is​ 95% confidence that the interval from minus 1.76 g divided by dL to minus 1.62 g divided by dL does not contain the value of the difference between the two population means left parenthesis mu 1 minus mu 2 right parenthesis .
c. Express the confidence interval with measures from men being population
1. and measures from women being population
2. Choose the correct answer below.
A. negative 1.62 g divided by dL less than mu 1 minus mu 2 less than 1.76 g divided by dL
B. negative 1.76 g divided by dL less than mu 1 minus mu 2 less than minus 1.62 g divided by dL
C. 1.62 g divided by dL less than mu 1 minus mu 2 less than 1.76 g divided by dL
D. negative 1.76 g divided by dL less than mu 1 minus mu 2 less than 1.62 g divided by dL.

Answer 1

(a) Because the confidence interval does not include includes 0​, it appears that there is not a significant difference between the mean level of hemoglobin in women and the mean level of hemoglobin in men.

(b) The correct option is (A).

(c) The correct option is (C).

Explanation:

The 95% confidence interval for the difference between the two population​ mean hemoglobin level is:

CI = (-1.76 < μ₁ - μ₂ < -1.62)

(a)

The hypothesis to test the equality of the mean hemoglobin level in women and the mean hemoglobin level in​ men is:

H₀: The two population means are equal, i.e. μ₁ = μ₂.

Hₐ: The two population means are not equal, i.e. μ₁ ≠ μ₂.

The (1 - α)% confidence interval can be used to draw conclusion about the hypothesis test.

Decision rule:

If the (1 - α)% confidence interval does not consist of the null value then the null hypothesis will be rejected and vice-versa.

The 95% confidence interval for the difference between the two population​ means is:

CI = (-1.76, -1.62)

The 95% confidence interval does not consist of the null value, i.e. 0.

Thus, the null hypothesis will be rejected.

"Because the confidence interval does not include includes 0​, it appears that there is not a significant difference between the mean level of hemoglobin in women and the mean level of hemoglobin in men."

(b)

The (1 - α)% confidence interval for population parameter implies that there is a (1 - α) probability that the true value of the parameter is included in the interval.

Or, the (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval.

So, the 95% confidence interval (-1.76, -1.62) implies that there is a 95% confidence that the above interval actually contains the value of the difference between the two population means, (μ₁ - μ₂).

The correct option is (A).

(c)

Now it is provided that the measures from men is denoted as population 1 and measures from women is denoted as population 2.

The confidence interval for the difference between two mean is:

`CI=(\bar x_(1)-\bar x_(2))\pm MOE`

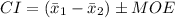
According to the information:

`\bar x_(1)=\bar x_(2)\\\\\bar x_(2)=\bar x_(1)`

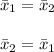
So, the new confidence interval will be:

`CI=-(\bar x_(2)-\bar x_(1))\pm MOE`

Then the confidence interval with measures from men being population

1 and measures from women being population 2 is:

`CI=(1.62<\mu_(1)-\mu_(2)<1.76)`

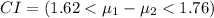
The correct option is (C).