Question

www.g The physical plant at the main campus of a large state university recieves daily requests to replace fluorescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 40 and a standard deviation of 8. Using the empirical rule, what is the approximate percentage of lightbulb replacement requests numbering between 24 and 40

Answer 1

`z=(24-40)/(8)=-2`

`z=(40-40)/(8)=0`

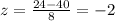
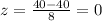
And then the percentage between 24 and 40 would be
`(95)/(2)= 47.5 \%`

Explanation:

For this problem we have the following parameters given:

`\mu = 40, \sigma =8`

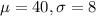
And for this case we want to find the percentage of lightbulb replacement requests numbering between 24 and 40.

From the empirical rule we know that we have 68% of the values within one deviation from the mean, 95% of the values within 2 deviations and 99.7% within 3 deviations.

We can find the number of deviations from themean for the limits with the z score formula we got:

`z=(X-\mu)/(\sigma)`

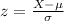
And replacing we got:

`z=(24-40)/(8)=-2`

`z=(40-40)/(8)=0`

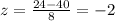
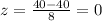
And then the percentage between 24 and 40 would be
`(95)/(2)= 47.5 \%`