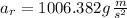Question

A centrifuge has an angular velocity of 3,000 rpm, what is the acceleration (in unit of the earth gravity) at a point with a radius of 10 cm

Answer 1

`a_(r) = 1006.382g \,(m)/(s^(2))`

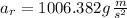
Step-by-step explanation:

Let suppose that centrifuge is rotating at constant angular speed, which means that resultant acceleration is equal to radial acceleration at given radius, whose formula is:

`a_(r) = \omega^(2)\cdot R`

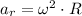
Where:

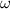`\omega` - Angular speed, measured in radians per second.

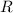`R` - Radius of rotation, measured in meters.

The angular speed is first determined:

`\omega = (\pi)/(30)\cdot \dot n`

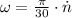
Where
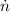`\dot n` is the angular speed, measured in revolutions per minute.

If
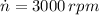`\dot n = 3000\,rpm`, the angular speed measured in radians per second is:

`\omega = (\pi)/(30)\cdot (3000\,rpm)`

`\omega \approx 314.159\,(rad)/(s)`

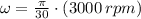
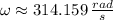
Now, if
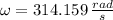`\omega = 314.159\,(rad)/(s)` and
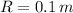`R = 0.1\,m`, the resultant acceleration is then:

`a_(r) = \left(314.159\,(rad)/(s) \right)^(2)\cdot (0.1\,m)`

`a_(r) = 9869.588\,(m)/(s^(2))`

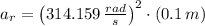
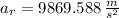
If gravitational acceleration is equal to 9.807 meters per square second, then the radial acceleration is equivalent to 1006.382 times the gravitational acceleration. That is:

`a_(r) = 1006.382g \,(m)/(s^(2))`