Question

A taut string of length 10 inches is plucked at the center. The vibration travels along the string at a constant rate of c inches per millisecond in both directions. If x represents the position on the string from the left-most end, so that 0≤x≤10, which of the following equations can be used to find the location x of the vibration after 0.3 milliseconds? A. | x -5 | =0. 3 B. ∣cx−5∣=0.3 C. | x -0.3 | = 5 D. | x - 10 | =0.3c

Answer 1

The correct option is

`A. \ (1)/(c) * \left | x - 5 \right | = 0.3`

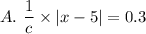
Explanation:

The parameters given are;

The length of the string = 10 inches

The speed or rate of travel of the wave = c inches per millisecond

The position on the string from the left-most end = x

The time duration of motion of the vibration to reach x= 0.3 milliseconds

The distance covered = Speed × Time = c×0.3

Given that the string is plucked at the middle, with the vibration travelling in both directions, the point after 0.3 millisecond is x where we have;

The location on the string where it is plucked = center of the string = 10/2 = 5 inches

Distance from point of the string being plucked (the center of the string) to the left-most end = 5 inches

Therefore, on the left side of the center of the string we have;

The distance from the location of the vibration x (measured from the left most end) to the center of the string = 5 - x = -(x -5)

On the right side of the center, the distance from x is -(5 - x) = x - 5

Therefore, the the equation that can be used to find the location of the vibration after 0.3 milliseconds is
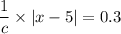`(1)/(c) * \left | x - 5 \right | = 0.3` or
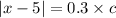`\left | x - 5 \right | = 0.3 * c` which gives the correct option as A