Question

What is the common ratio between successive terms in the sequence?

1

27, 9, 3, 1,

3.927

27

Answer 1

Question:

What is the common ratio between successive terms in the sequence?

27, 9, 3, 1

Answer:

common ratio =
`(1)/(3)`

Explanation:

In a geometric progression, the common ratio, r, is the ratio of a term in the sequence to a preceding term in that same sequence. In other words, the common ratio is found by dividing a term by the term just before it. For example, if the geometric sequence is:

a, b, c, d...

The common ratio is found by any of the following;

r =
`(b)/(a)` ----------(i)

r =
`(c)/(b)` -----------(ii)

r =
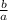`(d)/(c)` ------------(iii)

Any of equations (i) through (iii) will give the common ratio of the sequence.

============================================================

Now, from the question, the given sequence is;

27, 9, 3, 1

To get the common ratio, just divide the second term (9) by the first term (27) i.e

r =
`(9)/(27)` =
`(1)/(3)`

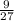OR

You can also divide the third term (3) by the second term (9). i.e

r =
`(3)/(9)` =
`(1)/(3)`

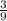OR

You can choose to divide the fourth term (1) by the third term (3). i.e

r =
`(1)/(3)`

Which ever adjacent terms you choose gives you the same result. Therefore, the common ratio of the given sequence is
`(1)/(3)`