Answer:
a.
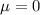 and
and
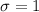
b. A bell-shaped curve (see the below graph).
c.
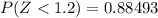
d.
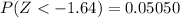
e.
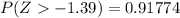
f.
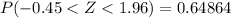
g.
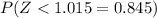 , c = 1.015.
, c = 1.015.
h.
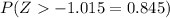 , c = -1.015.
, c = -1.015.
i.
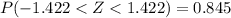
Explanation:
Z is a random variable and is a standardized value or a z-score. The formula for it is as follows:
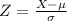 [1] (represented as a random variable)
[1] (represented as a random variable)
 [2] (represented as realizations of the random variables or values taken by the random variable Z.)
[2] (represented as realizations of the random variables or values taken by the random variable Z.)
Where
- The value
 is a realization of the random variable X, which is a raw score we want to standardize using [2].
is a realization of the random variable X, which is a raw score we want to standardize using [2].
 is the mean for the normally distributed data.
is the mean for the normally distributed data.
 is the standard deviation for the normally distributed data.
is the standard deviation for the normally distributed data.
Z follows a standard normal distribution (see formula [3]), which is a normal or Gaussian distribution with
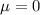 and
and
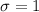 . It is symmetrical at
. It is symmetrical at
 [3]
[3]
Finding probabilities using the standard normal table
We can use the standard normal distribution to find all probabilities related to Z, and there exists the standard normal table, available in any Statistics books or on the Internet.
We need to consult the standard normal table, use the first two values for Z, that is, in the case of 1.64, we use 1.6 as an entry. We find this value in its first column, and then, using the first row of the table, we localize the remaining 0.04. The intersection of these two values "gives us" the cumulative probability from
 to the value z = 1.64.
to the value z = 1.64.
Notice that negative values for z-scores are below the mean, whereas positive values represent z-scores above
 .
.
Answering the questions
a. What is the mean and standard deviation for Z?
As we discuss before, the mean and the standard deviation are, respectively,
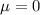 and
and
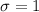 .
.
b. Sketch the distribution.
We can sketch it as a normal or Gaussian distribution, that is, a bell-shaped curve, symmetrical at
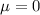 , with most values near the mean and less at each end of the distribution. See the below graph.
, with most values near the mean and less at each end of the distribution. See the below graph.
c. Find P(Z <1.2)
Following the explained procedure above, we can obtain the cumulative probability for
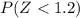 :
:
In the first column, we localize z = 1.2. At the first row, we localize the value 0.00 (since z = 1.2 = 1.20). Notice that this value is above the mean (positive).
Then, the asked probability is
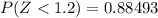 .
.
d. Find P(Z < −1.64)
The values less than z = -1.64 are below the mean, and we have for the first column z = -1.6 and for the first row -0.04. Then
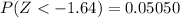
e. Find P(Z > −1.39)
In this case, we need to recall that
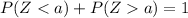
For any positive or negative value of a. Then
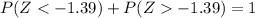
Thus
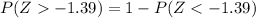
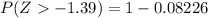
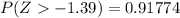
f. Find P(−0.45 < Z <1.96)
In this case, we need to find
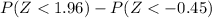 . Then
. Then
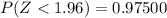
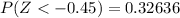
Therefore

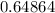
Then,
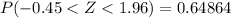 .
.
g. Find c such that P(Z < c) = 0.845
In this case, find the cumulative probability, 0.845, and the corresponding value for z.
This value is between z-scores (z = 1.01 and z = 1.02). The standard normal table cannot give us values for z with more than two decimal digits for z. We can overcome this using interpolation or technology, and this value will have a third digit for z. This value is approximately:
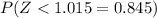 , c = 1.015.
, c = 1.015.
h. Find c such that P(Z > c) = 0.845
Because of the symmetry of the normal distribution:
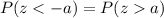 or
or
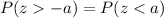
From the previous result (part g):
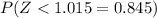
Then
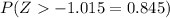 , c = -1.015.
, c = -1.015.
i. Find c such that P(−c < Z < c) = 0.845
We can overcome using the symmetry of the normal distribution again, and we know that 0.845 is a value between -c and c. At both extremes of the distribution we have symmetrically the following probabilities:
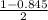
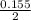
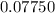
Then, we use
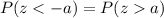
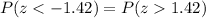
Then, approximately, c = 1.42 and -c = -1.42 or
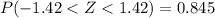 . Using linear interpolation or technology, we can have a value of c = 1.422 and -c = -1.422.
. Using linear interpolation or technology, we can have a value of c = 1.422 and -c = -1.422.