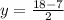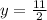Answer:
Solve for y in the first equation.
Explanation:
Given
3x+y=9
15x-3y = 1
Required
Determine the first step to avoid fractions
From the list of given options, the option that best answered the question is to Solve for y in the first equation.
Solving for y will let you substitute the expression for y in the second equation
Going by that:- Solve for y in the first equation.

Subtract 3x from both sides

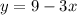
Substitute 9 - 3x for y in the second equation
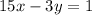 becomes
becomes
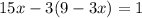
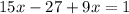
Collect like terms
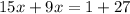
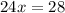
Divide both sides by 24
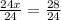

Divide numerator and denominator by 4

Substitute 7/6 for x in the
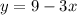
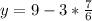

Solve fraction