Answer:
C. x - 3
Explanation:
Given the trinomial:
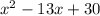
We factorize the trinomial to determine which of the given options is a factor.
Step 1: Multiply the first and last term of the trinomial.
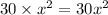
Step 2: Write out factor pairs of 30
Step 3: Determine which pair added together will give the middle term, -13
These are -3 and -10
Step 4: Replace -13x with -3x and -10x
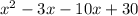
Step 5: Factorize
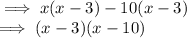
Therefore, one of the factors is x-3. The correct option is C.