Question

Select the correct answer
What is the inverse of the function f(x)=x+1/x

Answer 1

`{f}^( - 1) (x) = (1)/(x - 1)`

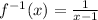
Option B is the correct option.

Explanation:

Let y = f ( x )

`y = (x + 1)/(x)`

Apply cross product property

`xy = x + 1`

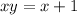
Move 'x' to L.H.S and change it's sign

`xy - x = 1`

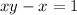
Take x as common

`x(y - 1) = 1`

`x = (1)/(y - 1)`

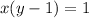
Replace x by f ⁻¹(x) and y by x

`{f}^( - 1) (x) = (1)/(x - 1)`

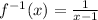
Hence, Option B is the correct option.

Hope this helps..

Best regards!!

Answer 2

`\boxed{\mathrm{B}}`

Explanation:

`f(x)=(x+1)/(x)`

`y=(x+1)/(x)`

Make x as subject.

Multiply both sides by x.

`yx=x+1`

Subtract both sides by x.

`yx-x=1`

Factor out x.

`x(y-1)=1`

Divide both sides by y-1.

`x=(1)/(y-1)`

Switch variables.

`y=(1)/(x-1)`