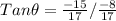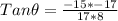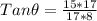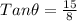Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s). Complete the statements below, simplify all ratios and keep them as improper fractions. If cos(θ) = and sin(θ) is negative, then sin(θ) = and tan(θ) = .

Answer 1

Question:

If cos(θ) =-8/17 and sin(θ) is negative, then sin(θ) = ___ and tan(θ) =___.

Answer:

`Sin\theta = (-15)/(17)`

`Tan\theta = (15)/(8)`

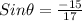
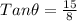
Explanation:

Given

cos(θ) =-8/17

Required

sin(θ) = __

tan(θ) =__

The first step is to determine the length of the third side

Given that

`cos(\theta) = (Adj)/(Hyp)`

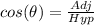
Where Adj and Hyp represent Adjacent and Hypotenuse

`cos(\theta) = (-8)/(17)`

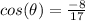
By comparison

`Adj = -8\ and\ Hyp = 17`

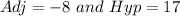
Using Pythagoras

`Hyp^2 = Adj^2 + Opp^2`

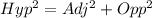
By Substitution

`17^2 = (-8)^2 + Opp^2`

`289 = 64 + Opp^2`

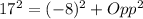
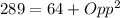
Subtract 64 from both sides

`289 - 64 = 64 - 64 + Opp^2`

`225 = Opp^2`

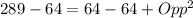
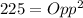
Take square roots of both sides

`√(225) = √(Opp^2)`

`√(225) = Opp`

`15 = Opp`

`Opp = 15`

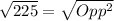
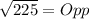
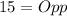
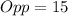
The question says that sin(θ) is negative; This implies that θ is in the third quadrant and as such

`Opp = -15`

From trigonometry

`Sin\theta = (Opp)/(Hyp)`

`Sin\theta = (-15)/(17)`

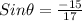
Also from trigonometry

`Tan\theta = Sin\theta / Cos\theta`

`Tan\theta = (-15)/(17) / (-8)/(17)`

`Tan\theta = (-15)/(17) * (-17)/(8)`

`Tan\theta = (-15 * -17)/(17 * 8)`

`Tan\theta = (15 * 17)/(17 * 8)`

`Tan\theta = (15)/(8)`