Question

Describe this pattern. Then see if you can think of another Pythagorean triple that doesn't follow the pattern you just described and that can't be generated using the identity (x2 − 1)2 + (2x)2 = (x2 + 1)2. Explain your findings. x-value Pythagorean Triple 7 (14,48,50) 8 (16,63,65) 9 (18,80,82) 10 (20,99,101)

Answer 1

See explanation

Explanation:

A Pythagorean triple is a set of 3 positive integer numbers, a, b, and c which satisfies the Pythagorean theorem:
`c^2=a^2+b^2`

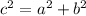
Given the identity:
`(x^2 - 1)^2 + (2x)^2 = (x^2 + 1)^2.`

We verify that the numbers given table are Pythagorean triples.

`14^2+48^2=2500=50^2\\16^2+63^2=4225=65^2\\18^2+80^2=6724=82^2\\20^2+99^2=10201=101^2`

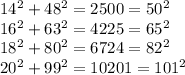
Next, we examine the pattern:

`\left|\begin{array}cx-value&x^2-1&2x&x^2 + 1&$Triple\\--&--&--&--&----\\7&48&14&50&(14,48,50)\\8&63&16&65&(16,63,65)\\9&80&18&82&(18,80,82)\\10&99&20&101&(20,99,101)\end{array}\right|`

From the pattern, our first number is 2x, the second number is x² - 1, and the third number(hypotenuse) is x² + 1

Next, we show that (x² - 1)² + (2x)² = (x² + 1)² is an identity

`LHS: (x^2 - 1)^2 + (2x)^2 \\= (x^2-1)(x^2-1)+2x^2\\=x^4-2x^2+1+4x^2\\=x^4+2x^2+1`

`RHS: (x^2+1)^2\\= (x^2+1) (x^2+1)\\=x^4+2x^2+1`

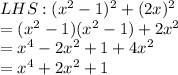
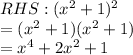
Since Left Hand Side=Right hand Side. For all x, the equation is always true.

Therefore, the pattern is true for any Pythagorean triple.