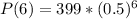Question

The half life of a radioactive substance is one day meaning that every day half of the substance has decayed . Suppose you have 399 grams of substance. Contract and exponential model for the amount of the substance remaining on given day. Use your model to determine how much of the substance will be left after 6 days

Answer 1

model:
`P(t) = 399 * (0.5)^t`

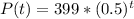
amount after 6 days:
`P(6) = 6.2344\ grams`

Explanation:

We can use the exponencial function of growth/decay to model this problem:

`P(t) = Po * (1 + r)^t`

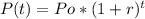
Where P(t) is the final value after time t, Po is the inicial value and r is the rate of change.

In our case, the inicial value is 399 grams, the rate is -0.5 (that is, the value decreases by half in each time cycle), and t is the time in days.

So our function will be:

`P(t) = 399 * (0.5)^t`

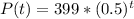
Then, to find the amount of substance after 6 days, we just need to calculate P using t = 6:

`P(6) = 399 * (0.5)^6`

`P(6) = 6.2344\ grams`