Question

Given: ∆KLM, KL ≅ LM A∈ KM , B ∈ KM AK ≅ BM Prove:△AKL ≅ △BML ΔALB is isosceles

Answer 1

m∠AKL=m∠BML | Base Angle Theorem (Base ∠ TH.)

Explanation:

KL=LM | Given

A ∈ KM | Given

B ∈ KM | Given

AK=BM | Given

m∠AKL=m∠BML | Base ∠ TH.

Answer 2

ΔAKL is congruent to ΔBML by the Side Angle Side rule of congruency and ΔALB is isosceles as two of its sides
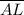`\overline {AL}` and
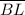`\overline {BL}` are congruent

Explanation:

The given parameters are;

The given triangle ΔKLM has sides
`\overline {KL}` ≅
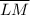`\overline {LM}`, Given

ΔKLM is isosceles Δ (two equal segments), Definition of isosceles Δ

∠LKM ≅ ∠LMK, Base ∠s of isosceles Δ are ≅

Point A is on segment
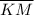`\overline {KM}`, Given

Point B is also on segment
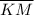`\overline {KM}`, Given

Segment
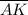`\overline {AK}` ≅ segment
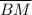`\overline {BM}`, Given

ΔAKL ≅ ΔBML, SAS rule of congruency

Segment
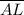`\overline {AL}` ≅ segment
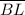`\overline {BL}`, CPCTC

ΔALB is isosceles (two equal segments), Definition of isosceles Δ

Where:

SAS = Side Angle Side

CPCTC = Congruent parts of congruent triangles are congruent.