Directions: Use the acronym PANIC to find the confidenceintervals.1.An SRS of 60 women showed that the average weight of a purse is 5 pounds with a standard deviation of 1.2 poun…

Question

asked Mar 15, 2021 216k views

1 Answer

Goulven · Answer 1 · 2021-03-20T02:46:59+0000

Answer:

90% Confidence Interval for the actual average weight of purses.

(4.7412 , 5.2588)

Explanation:

Explanation:-

Given sample size 'n' = 60

mean of the sample x⁻ = 5 pounds

Standard deviation of the sample 'S' = 1.2 pounds

Level of significance = 0.10

90% Confidence Interval for the actual average weight of purses.

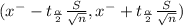
$(x^(-) - t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) +t_{(\alpha )/(2) } (S)/(√(n) ) )$

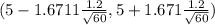
(5 - 1.6711(1.2)/(√(60) ) , 5 +1.671(1.2)/(√(60) ) )

( 5 - 0.2588 , 5 + 0.2588)

90% Confidence Interval for the actual average weight of purses.

(4.7412 , 5.2588)