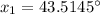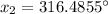Question

In the interval 0 x 360 find the values of x for which cos x =0.7252

Answer 1

`x_1 = 43.5145\°`

`x_2 = 316.4855\°`

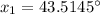
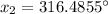
Explanation:

We have a positive value for the cosine of x, so we know that the value of x should be in the first quadrant (0 ≤ x ≤ 90) or in the fourth quadrant (270 ≤ x ≤ 360).

Now, let's find the value of x that gives cos(x) = 0.7252 using the inverse function of the cosine, that is, the arc cosine function.

The value of x can be calculated using:

`x = arccos(0.7252)`

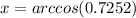
Using this function in a calculator (you may find it as:
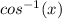`cos^(-1)(x)`), we have that:

`x_1 = 43.5145\°`

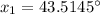
So this is the value of x in the first quadrant. To find the other value of x, in the fourth quadrant, that gives the same result, we just need to calculate 360° minus the value we found:

`x_2 = 360\° - 43.5145\° = 316.4855\°`

So the values of x are:

`x_1 = 43.5145\°`

`x_2 = 316.4855\°`