Question

Could you help me to solve the problem below the cost for producing x items is 50x+300 and the revenue for selling x items is 90x−0.5^2 the company makes is how much it takes in (revenue) minus how much it spends (cost).Recall that profit is revenue minus cost. Set up an expression for the profit from producing and selling x items. Find two values of x that will create a profit of $50. Is it possible for the company to make a profit of $2,500? Please explain

Answer 1

Profit function:
`P(x) = -0.5x^2 + 40x - 300`

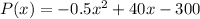
Values where the profit is $50:
`x_1 = 70`,
`x_2 = 10`

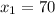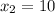
It is NOT possible to make a profit of $2,500, the maximum profit is $500.

Explanation:

To find the profit function P(x), we just need to calculate the revenue function R(x) minus the cost function C(x).

In our case, the cost function is:

`C(x) = 50x+300`

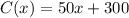
And the revenue function is:

`R(x) = 90x - 0.5x^2`

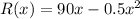
(I'm assuming this is the correct revenue and the question is missing an 'x' after 0.5 and before '^2')

So the profit function is:

`P(x) = R(x) - C(x)`

`P(x) = 90x - 0.5x^2 - 50x - 300`

`P(x) = -0.5x^2 + 40x - 300`

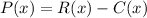
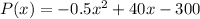
To find the values of x that give a profit of $50, we use P(x) = 50 and then find the values of x:

`50 = -0.5x^2 + 40x - 300`

`-0.5x^2 + 40x - 350 = 0`

`x^2 - 80x + 700 = 0`

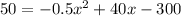
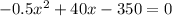
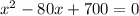
Using Bhaskara's formula, we have:

`\Delta = b^2 - 4ac = (-80)^2 - 4*1*700 = 3600`

`x_1 = (-b + √(\Delta))/2a = (80+60)/2 = 70`

`x_2 = (-b - √(\Delta))/2a = (80-60)/2 = 10`

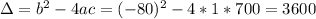
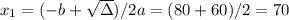
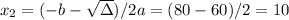
So the values of x area 10 and 70 items.

To find if it's possible to make a profit of $2,500, let's find the maximum value of our profit function.

We can find the value of x that gives the maximum profit finding the x of the vertex using this formula:

`x_v = -b/2a = 80/2 = 40`

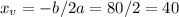
Now, using this value of x in the profit equation, we have the maximum profit:

`P(40) = -0.5*(40)^2 + 40*40 - 300 = 500`

The maximum profit of the company is $500, so it is not possible to make a profit of $2,500.