Question

PLEASE HELP

Choose the correct conic section to fit the equation.


y=1/8 x^2



1.Circle
2.Ellipse
3.Parabola
4.Hyperbola

Answer 1

Option (3)

Explanation:

Equations of the different conic sections are,

Circle → x² + y² = r²

Ellipse →
`(x^2)/(a^2)+(y^2)/(b^2)=1`

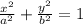
Parabola → y = ax²

Hyperbola →
`(x^2)/(a^2)-(y^2)/(b^2)=1`

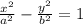
Given equation in the question is,

`y=(1)/(8)x^(2)`

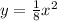
Which matches to the equation of a parabola,

y = ax²

Therefore, equation fits to a parabola.

Option (3) will be the answer.