Question

Select the correct answer from the drop-down menu. The graphed linear equation is . (a) 3x-2y=-12 (b)2x-3y=-12(c) 3x+2y=12(d)3x+3y=-12

Answer 1

c is the answer

Explanation:

3x+2y=12

Answer 2

Option (C) will be the answer.

Explanation:

Let the equation of the given line is,

y = mx + b

Where 'm' is the slope of the line and 'b' is the y-intercept

Slope of a line passing through two points (x₁, y₁) and (x₂, y₂) is represented by,

Slope of the line (m) =
`(y_2-y_1)/(x_2-x_1)`

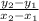
For a line passing through (0, 6) and (4, 0)

Slope 'm' =
`(6-0)/(0-4)`

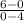
m =
`-(3)/(2)`

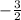
y-intercept of the line 'b' = 6

Therefore, equation of the line will be,

y =
`-(3)/(2)x+6`

2y = -3x + 12

3x + 2y = 12

Option (C) will be the answer.