The answer is likely choice C
The reason why I'm not entirely sure is because of a potential typo. See below.
Let's go through each answer choice
------------
Choice A
Solve each inequality for x
x+1 < -1 becomes x < -2 after subtracting 1 from both sides
x+1 < 1 becomes x < 0 after subtracting 1 from both sides
We have {x < -2} intersected with {x < 0}. The overlap is x < -2. I recommend using a number line diagram to see how the overlap is working. Basically we're looking for numbers that are both less than -2 AND also less than 0. That simplifies to numbers less than -2 (as anything less than -2 is already smaller than 0).
A number like x = -10 is in the solution set of {x < -2}, but we just wanted 0 and only 0 to be in the solution set. So we can rule out choice A.
------------
Choice B
Solve each for x
x+1 = 1 becomes x = 0
x+1 > 1 becomes x > 0
This is a contradiction as we're talking about numbers that are 0 itself and larger than 0 at the same time. No such number exists. Effectively, these two sets cannot be combined to make anything meaningful. In other words, the solution set here is the empty set. For this reason, we can rule out choice B
------------
Choice C
Again we solve each for x
x+1 < 1 becomes x < 0
x+1 > 1 becomes x > 0
This is also the empty set because there are no numbers both smaller than 0 and larger than 0 at the same time.
If we had "or equal to" as part of the inequality sign, then
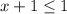 solves to
solves to
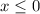 , while
, while
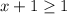 solves to
solves to
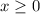 . Combining both
. Combining both
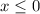 and
and
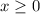 will yield exactly one item, and that is
will yield exactly one item, and that is
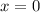
It seems like your teacher meant for this to be the answer and that there is a typo. Of course, its best to ask him/her about this directly.