Question

(a) (i) Find the probability of getting at least one 3 when 9 fair dice are thrown. (ii) When n fair dice are thrown, the probability of getting at least one 3 is greater than 0.9. Find the smallest possible value of n. (b) A bag contains 5 green balls and 3 yellow balls. Ronnie and Julie play a game in which they take turns to draw a ball from the bag at random without replacement. The winner of the game is the first person to draw a yellow ball. Julie draws the first ball. Find the probability that Ronnie wins the game.

Answer 1

(a)

(i) The probability of getting at least one 3 when 9 fair dice are thrown is 0.8062.

(ii) The value of n is 12.

(b) The probability that Ronnie wins the game is 0.3572.

Explanation:

(a)

(i)

The probability of getting a 3 on a single die roll is,
`p=(1)/(6)`.

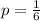It is provided that n = 9 fair dice are thrown together.

The outcomes of each die is independent of the others.

The random variable X can be defined as the number of die with outcome as 3.

The random variable X follows a Binomial distribution with parameters n = 9 and
`p=(1)/(6)`.

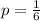Compute the probability of getting at least one 3 as follows:

`P(X\geq 1)=1-P(X=0)`

`=1-[{9\choose 0}((1)/(6))^(0)(1-(1)/(6))^(9-0)]\\\\=1-((5)/(6))^(9)\\\\=1-0.19381\\\\=0.80619\\\\\approx 0.8062`

Thus, the probability of getting at least one 3 when 9 fair dice are thrown is 0.8062.

(ii)

It is provided that:

P (X ≥ 1) > 0.90

Compute the value of n as follows:

`P (X \geq 1) > 0.90\\\\1-((5)/(6))^(n)>0.90\\\\((5)/(6))^(n)<0.10\\\\n\cdot \ln ((5)/(6))<\ln (0.10)\\\\n<(\ln (0.10))/(\ln (5/6))\\\\n<12.63\\\\n\approx 12`

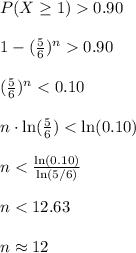
Thus, the value of n is 12.

(b)

It is provided that the bag contains 5 green balls and 3 yellow balls.

Ronnie and Julie play a game in which they take turns to draw a ball from the bag at random without replacement.

The winner of the game is the first person to draw a yellow ball.

Also provided that Julie draws the first ball.

P (Ronnie Wins) = P (The 1st yellow ball is selected at an even draw)

= P (The 1st yellow ball is drawn at 2nd, 4th and 6th draw)

= P (1st yellow ball is drawn at 2nd)

+ P (1st yellow ball is drawn at 4th)

+ P (1st yellow ball is drawn at 6th)

`=[(5)/(8)* (3)/(7)]+[(5)/(8)* (3)/(7)* (4)/(6)* (2)/(5)]+[(5)/(8)* (3)/(7)* (4)/(6)* (2)/(5)* (1)/(4)* 1]\\\\=0.2679+0.0714+0.0179\\\\=0.3572`

Thus, the probability that Ronnie wins the game is 0.3572.