Question

1. What percent of the players finished the walk in less than 2 hours? Show your work.

2. What is the probability that two randomly chosen players completed the walk in 2.9 hours or more? Show your work.


3. What is the probability that four randomly chosen players completed the walk between 1.7 and 2.9 hours? Show your work.


4. What observations can you make about the number of participants who complete the walk in more than 3.5 hours, given that there are 1,200 participants?


5. What might you observe if the number of participants increased or decreased?

Answer 1

The answer is given below

Explanation:

Suppose several high schools in a city are sponsoring a walk-athon to raise money for a local charity. A certain route is mapped out through the city and each participant finds sponsors to donate money for the walk. If a participant completes the walk under a certain time, extra money will be donated. You are responsible for recording the finishing times for each of the participants. After collecting all of the data, you determine that the finishing times are normally distributed with a mean of 2.6 hours and a standard deviation of 0.3 hour.

Answer:

Given that:

the mean μ = 2.6 hours and a standard deviation(σ) of 0.3 hour.

The z score is a measure used in probability to determine the number of standard deviation the raw score is above or below the mean, it is given by the equation:

`z=(x-\mu)/(\sigma)`

1) What percent of the players finished the walk in less than 2 hours.

To calculate this, we use x as 2 hours and then find the z score.

`z=(x-\mu)/(\sigma)=(2-2.6)/(0.3)=-2`

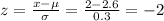
From the normal probability distribution table, P(x < 2) = P(z < -2) = 0.0228 = 2.28%

2) What is the probability that two randomly chosen players completed the walk in 2.9 hours or more

To calculate this, we use x as 2.9 hours and then find the z score.

`z=(x-\mu)/(\sigma)=(2.9-2.6)/(0.3)=1`

From the normal probability distribution table, P(x > 2.9) = P(z > 1) = 1-P(z<1) = 1 - 0.8413 = 0.1587

3. What is the probability that four randomly chosen players completed the walk between 1.7 and 2.9 hours

To calculate this, we first use x as 1.7 hours and then find the z score.

`z=(x-\mu)/(\sigma)=(1.7-2.6)/(0.3)=-3`

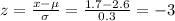
For x as 2.9 hours and then find the z score.

`z=(x-\mu)/(\sigma)=(2.9-2.6)/(0.3)=1`

From the normal probability distribution table, P(1.7 < x < 2.9) = P(-3 < z < 1) = P(z<1) - P(z < -3) = 0.8413 - 0.0013 = 0.84

4. What observations can you make about the number of participants who complete the walk in more than 3.5 hours, given that there are 1,200 participants?

To calculate this, we use x as 3.5 hours, number of samples (n) = 1200 and then find the z score.

`z=(x-\mu)/(\sigma/√(n) )=(3.5-2.6)/(0.3/√(1200) )=104`

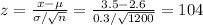
From the normal probability distribution table, P(x > 3.5) = P(z > 104) = 1-P(z<104) = 1 - 1 = 0

5. What might you observe if the number of participants increased or decreased?

if the number of participants increased , the probability would increase while if they decreased, the probability would decrease