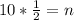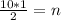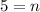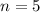Answer:
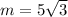
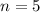
Explanation:
Given
The triangle above
Required
Find the missing lengths
The missing lengths can be calculated by applying trigonometry ratios
From the triangle above,
the Hypotenuse is 10
Angle = 60
Calculating m
The relationship between m, the Hypotenuse and angle 60 is defined as follows;
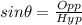
Where
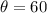
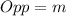
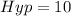
The above formula becomes
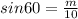
Multiply both sides by 10
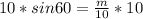
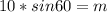
In radical from,
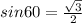
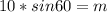 becomes
becomes
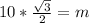
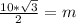
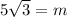
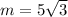
Calculating n
The relationship between n, the Hypotenuse and angle 60 is defined as follows;
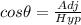
Where
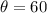
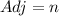
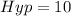
The above formula becomes
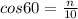
Multiply both sides by 10
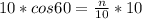
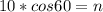
In radical from,
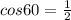
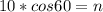 becomes
becomes