Answer:
The population of four years ago was 100,783 inhabitants
Explanation:
The population of the city after t years is given by the following equation:

In which P(0) is the initial population and r is the decrease rate, as a decimal.
2 years later, that is to say two years ago, the population of this same city was 81,000 inhabitants and today it is 65,610.
This means that:

We are going to use this to build a system, and find P(0), which is the initial population(four years ago).
P(2) = 81000


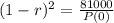
P(4) = 65610

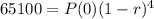
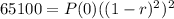
Since
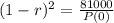
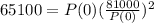
Using P(0) = x

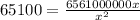
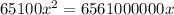
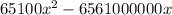
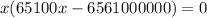
x = 0, which does not interest us, or:
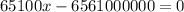
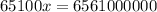


The population of four years ago was 100,783 inhabitants