Answer:
Check below
Explanation:
Hi there. These are operations with functions. So Let's work with these functions.
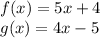
1.
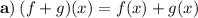
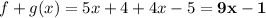
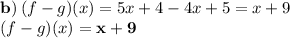
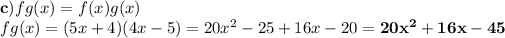
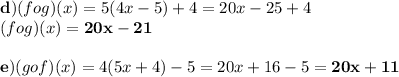
2) Domain
a) The Domain of these functions is defined as the intersection of the first function's Domain f(x) and g(x)'s domain:
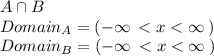
So the Domain of (f+g)(x),(f-g), and (fg)(x): Real set.
The functions have no discontinuity, nor restrictions.