Answer:
There are
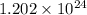 atoms and
atoms and
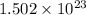 molecules in the compound.
molecules in the compound.
Step-by-step explanation:
The molar mass of the sulphur is
 . The Avogradro's Law states that exists
. The Avogradro's Law states that exists
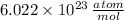 . The quantity of atoms in a quantity of mass is derived from dividing the mass by the molar mass and multiplying it by the Avogadro's Number. That is:
. The quantity of atoms in a quantity of mass is derived from dividing the mass by the molar mass and multiplying it by the Avogadro's Number. That is:
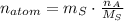
Where:
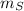 - Mass of the sample, measured in grams.
- Mass of the sample, measured in grams.
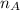 - Avogadro's Number, measured in atoms per mole.
- Avogadro's Number, measured in atoms per mole.
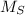 - Molar mass of the sulphur, measured in grams per mole.
- Molar mass of the sulphur, measured in grams per mole.
If
 ,
,
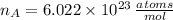 and
and
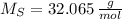 , then:
, then:
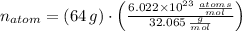

There are
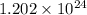 atoms in the compound.
atoms in the compound.
Now, the molecular weight of the compound is:
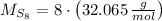
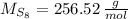
The quantity of molecules in a quantity of mass is derived from dividing the mass by the molecular weight and multiplying it by the Avogadro's Number. That is:
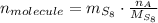
Where:
 - Mass of the sample, measured in grams.
- Mass of the sample, measured in grams.
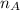 - Avogadro's Number, measured in atoms per mole.
- Avogadro's Number, measured in atoms per mole.
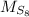 - Molecular weight of the compound (octosulphur), measured in grams per mole.
- Molecular weight of the compound (octosulphur), measured in grams per mole.
If
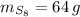 ,
,
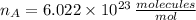 and
and
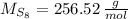 , then:
, then:
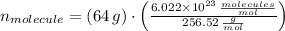
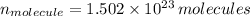
There are
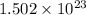 molecules in the compound.
molecules in the compound.