Question

When p = 12, t = 2, and s = One-sixth, r = 18. If r varies directly with p and inversely with the product of s and t, what is the constant of variation?

Answer 1

b

Explanation:

Answer 2

`k = (1)/(2)`

Explanation:

Given

`p = 12`

`t = 2`

`s = (1)/(6)`

`r = 18`

`r\ \alpha\ p\ * (1)/(s * t)`

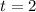
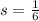
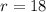
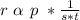
Required

Find the constant of variation

From the question, the variation is as follows

`r\ \alpha\ p\ * (1)/(s * t)`

`r\ \alpha\ (p * 1)/(s * t)`

`r\ \alpha\ (p)/(s * t)`

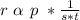
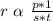
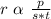
Convert variation to equation

`r\ = k(p)/(s * t)`

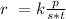
Where k represents the constant of variation

Make k the subject of formula;

Multiply both sides by s * t

`r * s * t = k(p)/(s * t) * s * t`

`r * s * t = kp`

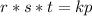
Divide both sides by p

`(r * s * t)/(p) = (kp)/(p)`

`(r * s * t)/(p) = k`

`k = (r * s * t)/(p)`

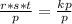
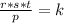
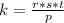
Substitute the values of p, r, s and t in the above equation

`k = (18 * (1)/(6) * 2)/(12)`

`k = (6)/(12)`

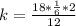
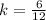
Divide numerator and denominator by 6

`k = (1)/(2)`

Hence, the constant of variation is;
`k = (1)/(2)`