Answer:
The frequency of oscillations is 7 Hz
Step-by-step explanation:
Given;
mass of car, = 1700 kg
mass of driver, = 66 kg
compression of the spring, x = 5mm = 0.005 m
The frequency of the oscillation is given as;
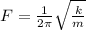
where;
k is force constant
m is the total mass of the car and the driver
m = 1700 kg + 66 kg = 1766 kg
Weight of the car and the driver;
W = mg
W = 1766 x 9.8
W = 17306.8 N
Apply hook's law, to determine the force constant;
F = kx
W = F
Thus, k = W/x
k = 17306.8 / 0.005
k = 3461360 N/m
Now, calculate the frequency
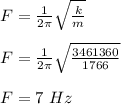
Therefore, the frequency of oscillations is 7 Hz