Question

Before the pandemic cancelled sports, a baseball team played home games in a stadium that holds up to 50,000 spectators. When ticket prices were set at $12, the average attendance was 30,000. When the ticket prices were on sale for $10, the average attendance was 35,000.

(a) Let D(x) represent the number of people that will buy tickets when they are priced at x dollars per ticket. If D(x) is a linear function, use the information above to find a formula for D(x). Show your work!
(b) The revenue generated by selling tickets for a baseball game at x dollars per ticket is given by R(x) = x-D(x). Write down a formula for R(x).
(c) Next, locate any critical values for R(x). Show your work!
(d) If the possible range of ticket prices (in dollars) is given by the interval [1,24], use the Closed Interval Method from Section 4.1 to determine the ticket price that will maximize revenue. Show your work!
Optimal ticket price:__________ Maximum Revenue:___________

Answer 1

(a)
`D(x)=-2,500x+60,000`

(b)
`R(x)=60,000x-2500x^2`

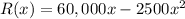
(c) x=12

(d)Optimal ticket price: $12

Maximum Revenue:$360,000

Explanation:

The stadium holds up to 50,000 spectators.

When ticket prices were set at $12, the average attendance was 30,000.

When the ticket prices were on sale for $10, the average attendance was 35,000.

(a)The number of people that will buy tickets when they are priced at x dollars per ticket = D(x)

Since D(x) is a linear function of the form y=mx+b, we first find the slope using the points (12,30000) and (10,35000).

`\text{Slope, m}=(30000-35000)/(12-10)=-2500`

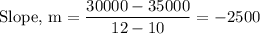
Therefore, we have:

`y=-2500x+b`

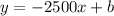
At point (12,30000)

`30000=-2500(12)+b\\b=30000+30000\\b=60000`

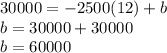
Therefore:

`D(x)=-2,500x+60,000`

(b)Revenue

`R(x)=x \cdot D(x) \implies R(x)=x(-2,500x+60,000)\\\\R(x)=60,000x-2500x^2`

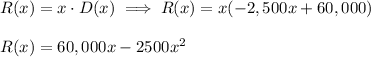
(c)To find the critical values for R(x), we take the derivative and solve by setting it equal to zero.

`R(x)=60,000x-2500x^2\\R'(x)=60,000-5,000x\\60,000-5,000x=0\\60,000=5,000x\\x=12`

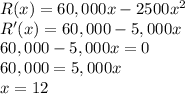
The critical value of R(x) is x=12.

(d)If the possible range of ticket prices (in dollars) is given by the interval [1,24]

Using the closed interval method, we evaluate R(x) at x=1, 12 and 24.

`R(x)=60,000x-2500x^2\\R(1)=60,000(1)-2500(1)^2=\$57,500\\R(12)=60,000(12)-2500(12)^2=\$360,000\\R(24)=60,000(24)-2500(24)^2=\$0`

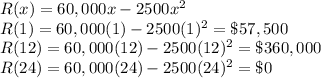
Therefore:

• Optimal ticket price:$12
• Maximum Revenue:$360,000