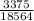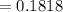Question

Eighteen telephones have just been received at an authorized service center. Six of these telephones are cellular, six are cordless, and the other six are corded phones. Suppose that these components are randomly allocated the numbers 1, 2, . . . , 18 to establish the order in which they will be serviced. (Round your answers to four decimal places.)

(a) What is the probability that all the cordless phones are among the first twelve to be serviced?
(b) What is the probability that after servicing twelve of these phones, phones of only two of the three types remain to be serviced?
(c) What is the probability that two phones of each type are among the first six serviced?

Answer 1

a) 0.0498

b) 0.1489

c) 0.1818

Explanation:

Given:

Number of telephones = 6+6+6= 18

6 cellular, 6 cordless, and 6 corded.

a) Probability that all the cordless phones are among the first twelve to be serviced:

12 are selected from 18 telephones, possible number of ways of selection = ¹⁸C₁₂

Then 6 cordless telephones are serviced, the remaining telephones are: 12 - 6 = 6.

The possible ways of selecting thr remaining 6 telephones = ¹²C₆

Probability of servicing all cordless phones among the first twelve:

= (⁶C₆) (⁶C₁₂) / (¹⁸C₁₂)

`= (1 * 924)/(18564)`

`= 0.0498`

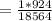
b) Probability that after servicing twelve of these phones, phones of only two of the three types remain to be serviced:

Here,

One type must be serviced first

The 6 remaining to be serviced can be a combination of the remaining two types.

Since there a 3 ways to select one type to be serviced, the probability will be:

= 3 [(⁶C₁)(⁶C₅) + (⁶C₂)(⁶C₄) + (⁶C₃)(⁶C₃) + (⁶C₄)(⁶C₂) + (⁶C₅)(⁶C₁)] / ¹⁸C₁₂

`= (3 * [(6)(6) + (15)(15) + (20)(20) + (15)(15) + (6)(6)])/(18564)`

`= (2766)/(18564)`

`= 0.1489`

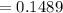
c) probability that two phones of each type are among the first six:

(⁶C₂)³/¹⁸C₆

`(3375)/(18564)`

`=0.1818`