Question

A Ferris wheel starts at rest and builds up to a final angular speed of 0.70 rad/s while rotating through an angular displacement of 4.9 rad. What is its average angular acceleration

Answer 1

The average angular acceleration is 0.05 radians per square second.

Step-by-step explanation:

Let suppose that Ferris wheel accelerates at constant rate, the angular acceleration as a function of change in angular position and the squared final and initial angular velocities can be clear from the following expression:

`\omega^(2) = \omega_(o)^(2) + 2 \cdot \alpha\cdot (\theta-\theta_(o))`

Where:

`\omega_(o)`,
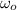`\omega` - Initial and final angular velocities, measured in radians per second.

`\alpha` - Angular acceleration, measured in radians per square second.

`\theta_(o)`,
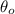`\theta` - Initial and final angular position, measured in radians.

Then,

`\alpha = (\omega^(2)-\omega_(o)^(2))/(2\cdot (\theta-\theta_(o)))`

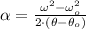
Given that
`\omega_(o) = 0\,(rad)/(s)`,
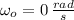`\omega = 0.70\,(rad)/(s)` and
`\theta-\theta_(o) = 4.9\,rad`, the angular acceleration is:

`\alpha = (\left(0.70\,(rad)/(s) \right)^(2)-\left(0\,(rad)/(s) \right)^(2))/(2\cdot \left(4.9\,rad\right))`

`\alpha = 0.05\,(rad)/(s^(2))`

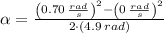
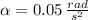
Now, the time needed to accelerate the Ferris wheel uniformly is described by this kinematic equation:

`\omega = \omega_(o) + \alpha \cdot t`

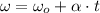
Where
`t` is the time measured in seconds.

The time is cleared and obtain after replacing every value:

`t = (\omega-\omega_(o))/(\alpha)`

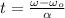
If
`\omega_(o) = 0\,(rad)/(s)`,
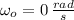`\omega = 0.70\,(rad)/(s)` and
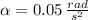`\alpha = 0.05\,(rad)/(s^(2))`, the required time is:

`t = (0.70\,(rad)/(s) - 0\,(rad)/(s) )/(0.05\,(rad)/(s^(2)) )`

`t = 14\,s`

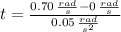
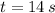
Average angular acceleration is obtained by dividing the difference between final and initial angular velocities by the time found in the previous step. That is:

`\bar \alpha = (\omega-\omega_(o))/(t)`

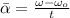
If
`\omega_(o) = 0\,(rad)/(s)`,
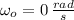`\omega = 0.70\,(rad)/(s)` and
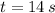`t = 14\,s`, the average angular acceleration is:

`\bar \alpha = (0.70\,(rad)/(s) - 0\,(rad)/(s) )/(14\,s)`

`\bar \alpha = 0.05\,(rad)/(s^(2))`

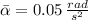
The average angular acceleration is 0.05 radians per square second.