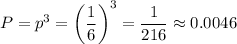Answer:
The probability that a player will receive such a penalty on any given turn is P=0.0046 or 1 chance in 216.
Explanation:
Each roll involves two six-sided dice.
If we get the same value in both dice, the player is allowed to roll again.
We will have a penalty if we get the same value in both dices three times in a row.
First, we have to calculate the probability of getting the same value in both dices.
The possible outcomes are 6^2=36. There are only 6 numbers, so there are only 6 possible outcomes that have the same value.
Then, the probability of this event is:

Now, we can calculate the probability of having this event three times in a row. This can be calculated as: