Answer:
0.230
Explanation:
Given
Estimate = 72%
Number of citizens = 14
Required
Find the probability that exactly 10 of the citizens will be in favor
This question can be solved using binomial expansion of probability which states;
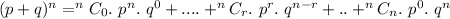
Where p and q are the probabilities of those in favor and against of building a health center;
n is the selected sample and r is the sample in favor
So; from the above analysis
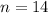
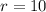
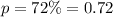
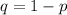
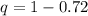
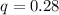
Since, we're solving for the probability that exactly 10 citizens will be in favor;
we'll make use of
Substituting these values in the formula above
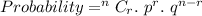

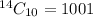
So, the expression becomes
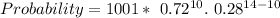
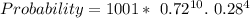
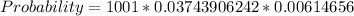
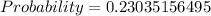
 ----Approximated
----Approximated
Hence, the probability that exact;y 10 will favor the building of the health center is 0.230