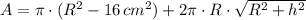Answer:
The surface area of the piece of wood to be painted is:
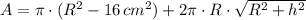
Explanation:
The surface area to be painted is equal to the surface area of the cone minus the cross area of the hole. That is:
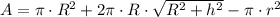
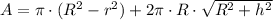
Where:
 - Radius at the bottom of the cylinder, measured in centimeters.
- Radius at the bottom of the cylinder, measured in centimeters.
 - Height of the cylinder, measured in centimeters.
- Height of the cylinder, measured in centimeters.
 - Radius of the cylindrical hole, measured in centimeters.
- Radius of the cylindrical hole, measured in centimeters.
If
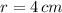 , the surface area of the piece of wood to be painted is:
, the surface area of the piece of wood to be painted is: