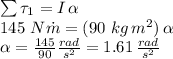Answer:
the angular acceleration of the gate is approximately 1.61
Step-by-step explanation:
Recall the formula that connects the net torque with the moment of inertia of a rotating object about its axis of rotation, and the angular acceleration (similar to Newton's second law with net force, mass, and linear acceleration):
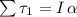
In our case, both forces contribute to the same direction of torque, so we can add their torques up and get the net torque on the gate:
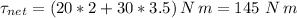
Now we use this value to obtain the angular acceleration by using the given moment of inertia of the rotating gate: