Answer:

Step-by-step explanation:
Hello,
In this case, since pressure is defined as the force applied over a surface:
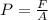
We can associate the force with the weight of the needle computed by using the acceleration of the gravity:
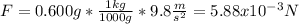
And the area of the the tip (circle) in meters:

Thus, the pressure exerted on the record turns out:
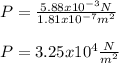
Which is truly a large value due to the tiny area on which the pressure is exerted.
Best regards.