Question

A car is running at the speed of 45km/hr see a child 25 meter ahead and suddenly apllies a brakes. If the retradation of the car is 2 meter per second square,is the child spared?

Answer 1

The car stops in 7.78s and does not spare the child.

Step-by-step explanation:

In order to know if the car stops before the distance to the child, you take into account the following equation:

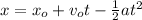`x=x_o+v_ot-(1)/(2)at^2` (1)

vo: initial speed of the car = 45km/h

a: deceleration of the car = 2 m/s^2

t: time

xo: initial distance to the child = 25m

x: final distance to the child = 0m

It is necessary that the solution of the equation (1) for time t are real.

You first convert the initial speed to m/s, then replace the values of the parameters and solve the quadratic polynomial for t:

`45(km)/(h)*(1h)/(3600s)*(1000m)/(1km)=12.5(m)/(s)`

`0=25+12.5t-2t^2\\\\2t^2-12.5t-25=0\\\\t_(1,2)=(-(-12.5)\pm √((-12.5)^2-4(2)(-25)))/(2(2))\\\\t_(1,2)=(12.25\pm 18.87)/(4)\\\\t_1=7.78s\\\\t_2=-1.65s`

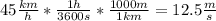
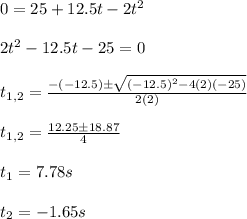
You take the first value t1 because it has physical meaning.

The solution for t is real, then, the car stops in 7.78s and does not spare the child.