Question

A company manufactures two products. For $1.00 worth of product A, the company spends $0.40 on materials, $0.20 on labor, and $0.10 on overhead. For $1.00 worth of product B, the company spends $0.50 on materials, $0.20 on labor, and $0.15 on overhead.

Let
a = (0.40, 0.20, 0.10) b = (0.50, 0.20, 0.15)
Then a and b represent the "costs per dollar of income" for the two products. Suppose the company manufactures x dollars worth of product A and y dollars worth of product B and that its total costs for materials are $260, its total costs for labor are $120, and its total costs for overhead are $70.
Determine x and y, the dollars worth of each product produced.

Answer 1

x = $400, y = $200

Step-by-step explanation:

`a = \left[\begin{array}{ccc}0.4\\0.2\\0.1\end{array}\right]\\b = \left[\begin{array}{ccc}0.5\\0.2\\0.15\end{array}\right]`

`xa + yb = \left[\begin{array}{ccc}260\\120\\70\end{array}\right] \\x \left[\begin{array}{ccc}0.4\\0.2\\0.1\end{array}\right] + y \left[\begin{array}{ccc}0.5\\0.2\\0.15\end{array}\right] = \left[\begin{array}{ccc}260\\120\\70\end{array}\right]`

`\left[\begin{array}{ccc}0.4&0.5\\0.2&0.2\\0.1&0.15\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}260\\120\\70\end{array}\right]\\\\\left[\begin{array}{ccc}0.1&0.15\\0.2&0.2\\0.4&0.5\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}70\\120\\260\end{array}\right]\\`

Perform the following operation on the matrix equation above:

`R_2 \rightarrow R_2 - 2R_1\\R_3 \rightarrow R_3 - 4R_1`

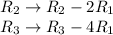
The result becomes:

`\left[\begin{array}{ccc}0.1&0.15\\0&-0.1\\0&-0.1\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}70\\-20\\-20\end{array}\right]\\`

Perform the following operation on the matrix equation above:

`R_3 \rightarrow R_3 - R_2`

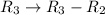
`\left[\begin{array}{ccc}0.1&0.15\\0&-0.1\\0&0\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}70\\-20\\0\end{array}\right]\\\left[\begin{array}{ccc}0.1&0.15\\0&-0.1\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}70\\-20\end{array}\right]`

From the matrix equation above:

0.1x + 0.15y = 70.........(1)

-0.1y = -20.............(2)

From equation (2)

y = (-20)/(-0.1)

y = $200

Put the value of y into equation (1)

0.1x + 0.15(200) = 70

0.1x = 40

x = 40/0.1

x = $400